Binary Search Trees

Binary Search Tree

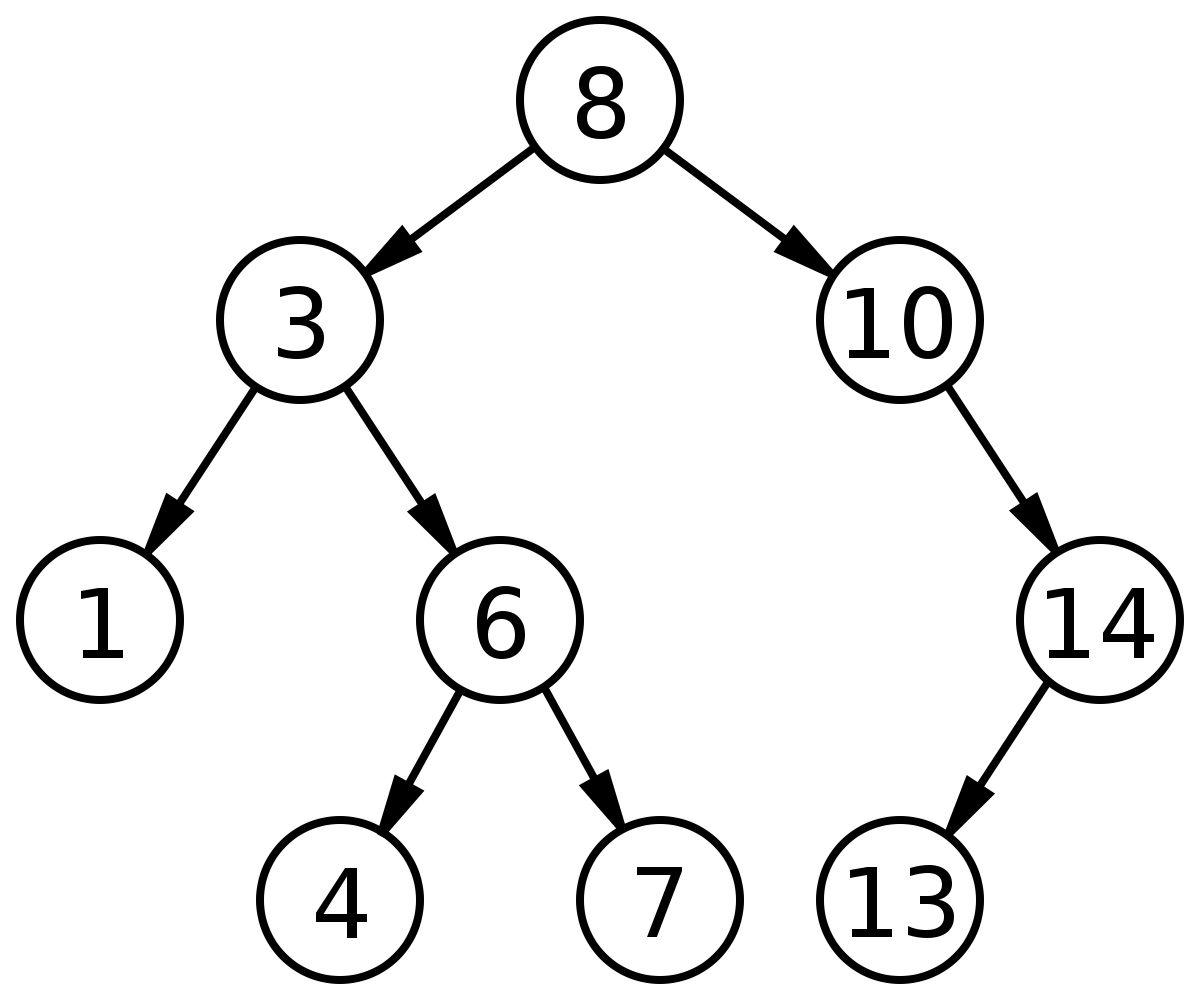
A Binary Search Tree (BST) is a hierarchical data structure with the following properties:

Each node has at most two children, referred to as the left child and the right child.
The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.

This structure allows for efficient searching, insertion, and deletion operations, typically with an average time complexity of O(log n) in balanced trees.

Traversal of a binary tree

Pre Order: Root, Left, Right (8,3,1,6,4,7,10,14,13)
Inorder: Left, Root, Right (1,3,4,6,7,8,10,13,14)
Post Order: Left, Right, Root (1,4,7,6,3,13,14,10,8)

Nomenclature

Degree: Number of nodes connected to any specific node
Level: The root node starts at level 0, and increases by 1 as you go down each level
Max Depth: Max number of edges (links) from root to a leaf node
1. Node 8 (root): depth 0
2. Nodes 3 and 10: depth 1
3. Nodes 1, 6, and 14: depth 2
4. Nodes 4, 7, and 13: depth 3
Height: The number of edges on the longest path from root to a leaf node

Time Complexity

Searching

Average Case: O(log n)
Worst Case: O(n)

Searching in a BST typically involves traversing from the root to a leaf, comparing the target value with each node. In a balanced tree, this process eliminates half the remaining nodes at each step, resulting in O(log n) complexity. However, in an unbalanced tree that degenerates into a linked list, the worst-case time complexity becomes O(n)

Insertion

Average Case: O(log n)
Worst Case: O(n)

Insertion follows a similar path to searching, as it needs to find the correct position to place the new node. In a balanced tree, this operation takes O(log n) time on average. However, if the tree becomes unbalanced due to the order of insertions, the worst-case time complexity can degrade to O(n).

Deletion

Average Case: O(log n)
Worst Case: O(n)

Deletion is slightly more complex but generally has the same time complexity as insertion and searching. The process involves finding the node to delete (O(log n) in balanced trees) and then handling three possible cases

Deleting a leaf node
Deleting a ndoe with one child
Deleting a node with two children

The third case is the most complex, often involving finding the in-order successor or predecessor. Despite this, the overall time complexity remains O(log n) for balanced trees and O(n) in the worst case for unbalanced trees.

It's important to note that these time complexities assume a basic, unbalanced BST. Self-balancing BSTs like AVL trees or Red-Black trees maintain balance through rotations, ensuring O(log n) worst-case time complexity for all operations.

Pre Order, in order, post order traversal

Trees